说明¶

真实函数：$f(x)=10sin0.6x , x\in[-7,7)$
测试数据集：$\{(x,y)|y=f(x)+rd.uniform(-1.5,1.5)rd.gauss(0,5),x为[-7,7)内120个均匀分布点\}$
分段个数：Partition=6
评价函数
1. $f_1$:分段测试函数的mse
2. $f_2$:在f1基础上增加间断点连续性和平滑性判断指标，影响连续性的参数$\alpha=0.01$，影响平滑性的参数$\beta$取$\frac {\pi}{18}$

实验¶

分段数据集下拟合比较¶

在原数据集集成商均匀划分6段，每段20个数据点单独cma拟合，绘制的曲线记作$div$与$f_1$比较

import makeData as md
import pandas as pd
import numpy as np
%pylab
plt.rc('figure', figsize=(16, 9))

Using matplotlib backend: MacOSX
Populating the interactive namespace from numpy and matplotlib

L=[]
SL=14.0/6
for i in range(6):
    L.append(-7+(i+1)*SL-0.01)
def realLineFunc(param):
    def f(x):
        i=int(math.floor((x+7)/SL))
        return np.poly1d(param[3*i:3*(i+1)])(x)
    return f
def draw1(title):
    ps=md.loadData('data1.tl')
    x=ps[0]
    y=ps[1]
    res=md.loadData('result.tl')
    cres=[]
    t1=0
    for v in res.values():
        cres=np.append(cres,v['param'])
        t1+=v['iter']
    res1=md.loadData('corres.tl')
    cres1=res1['param']
    d={'div总迭代次数':pd.Series(t1),
      'f1迭代次数':pd.Series(res1['iter']),}
    print pd.DataFrame(d)
    plt.figure(1)
    plt.plot(x,y,'b.',alpha=0.6,label="measure point")
    plt.plot(x,map(lambda x:10*math.sin(0.6*x),x),c="cyan",lw=2,ls="-",alpha=0.7,label="real function")
    x1=np.insert(x,0,L)
    x1.sort()
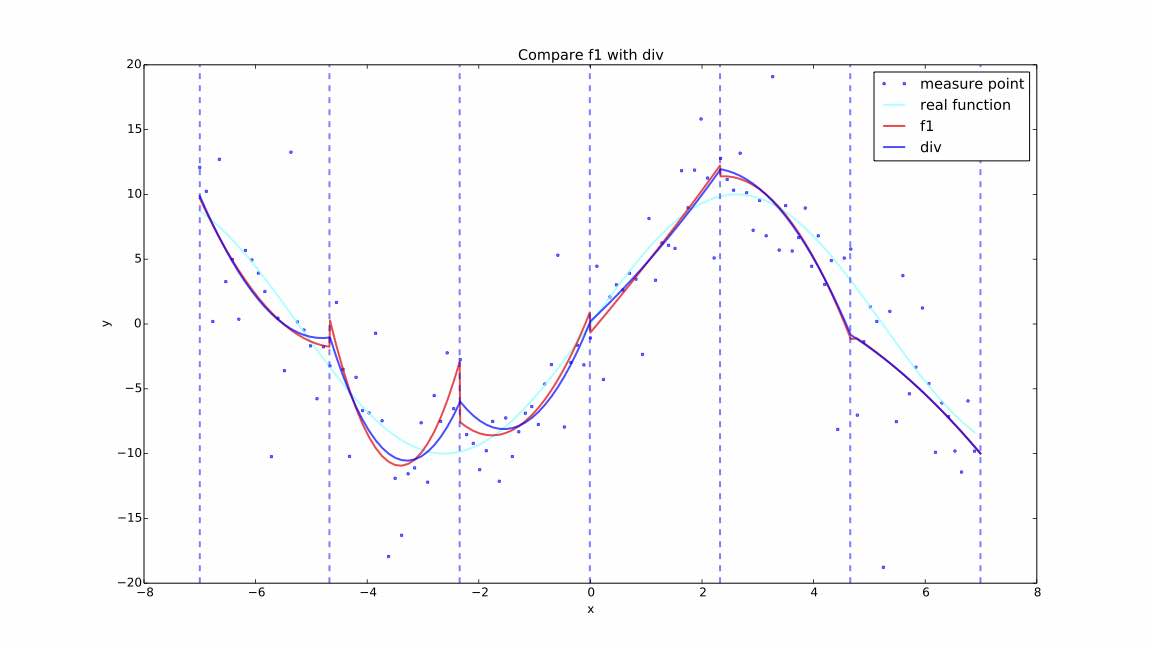
    plt.plot(x1,map(realLineFunc(cres),x1),c="red",lw=2,ls="-",alpha=0.7,label="f1")
    plt.plot(x1,map(realLineFunc(cres1),x1),c="blue",lw=2,ls="-",alpha=0.7,label="div")
    L.append(-7)
    for l in L:
        plt.plot([l,l],[-20,20],'b--',lw=2,alpha=0.5)
    plt.legend(loc='best')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.title(title)
    plt.show()

draw1('Compare f1 with div')

   div总迭代次数  f1迭代次数
0       514    2135

利用div参数结果$\sigma$扰动近似拟合¶

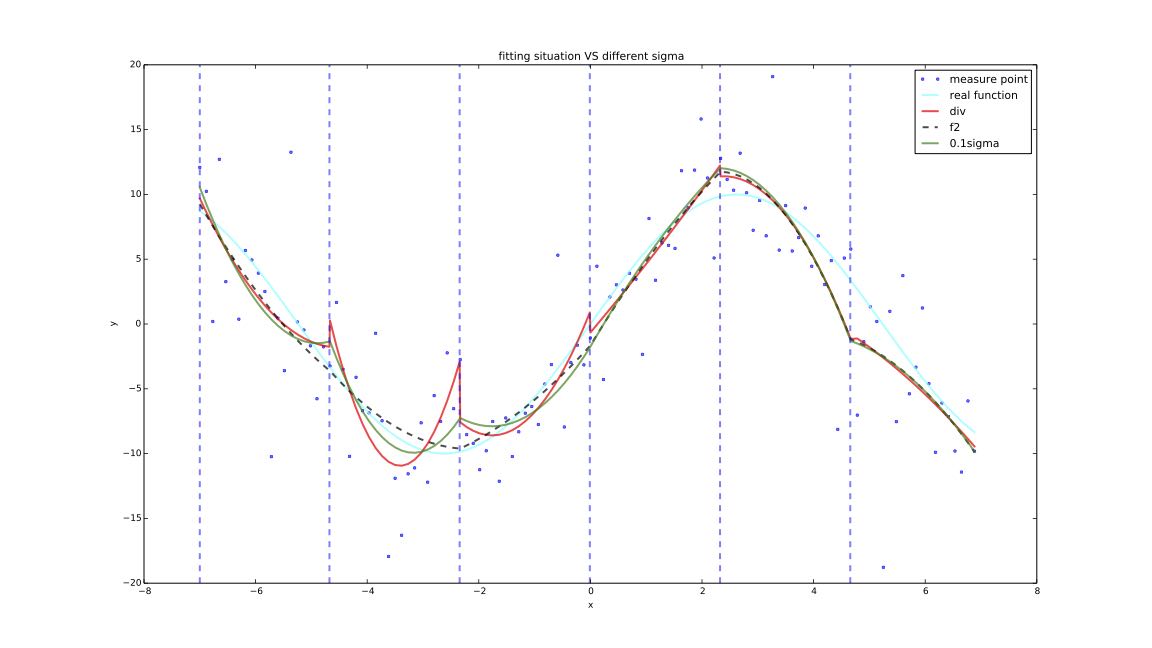
$\sigma=0.1$，迭代次数为2344 $$拟合情况接近f2，但代价也接近 $$
$\sigma=0.01$，迭代次数为2311
$$拟合情况接近f2，但代价也接近 $$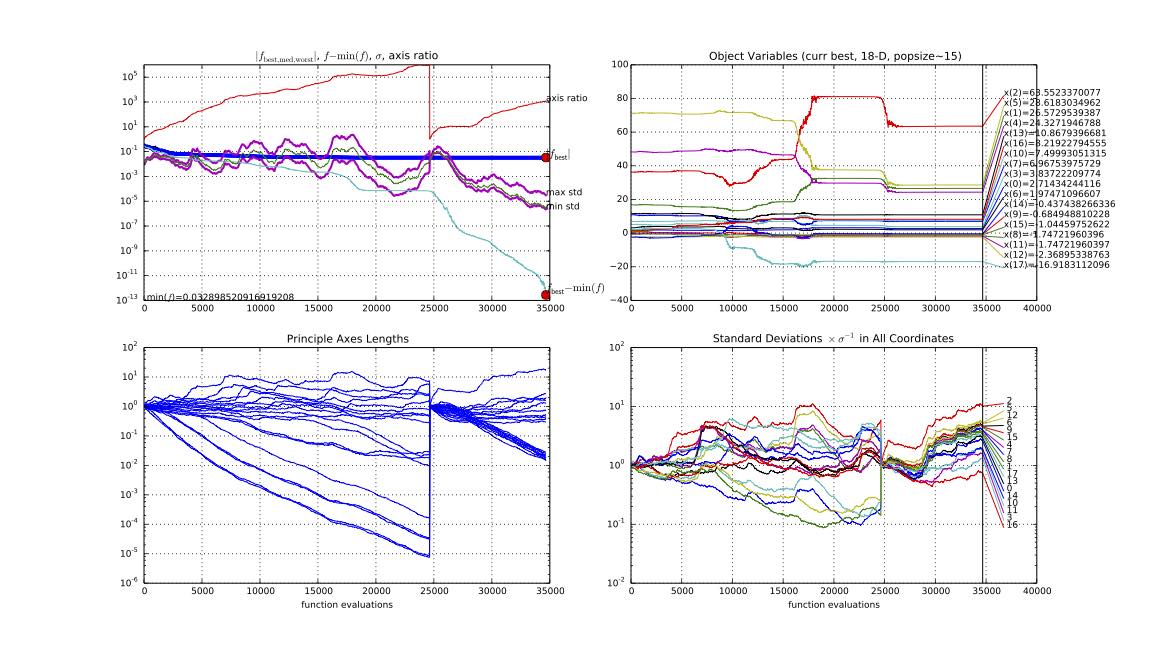
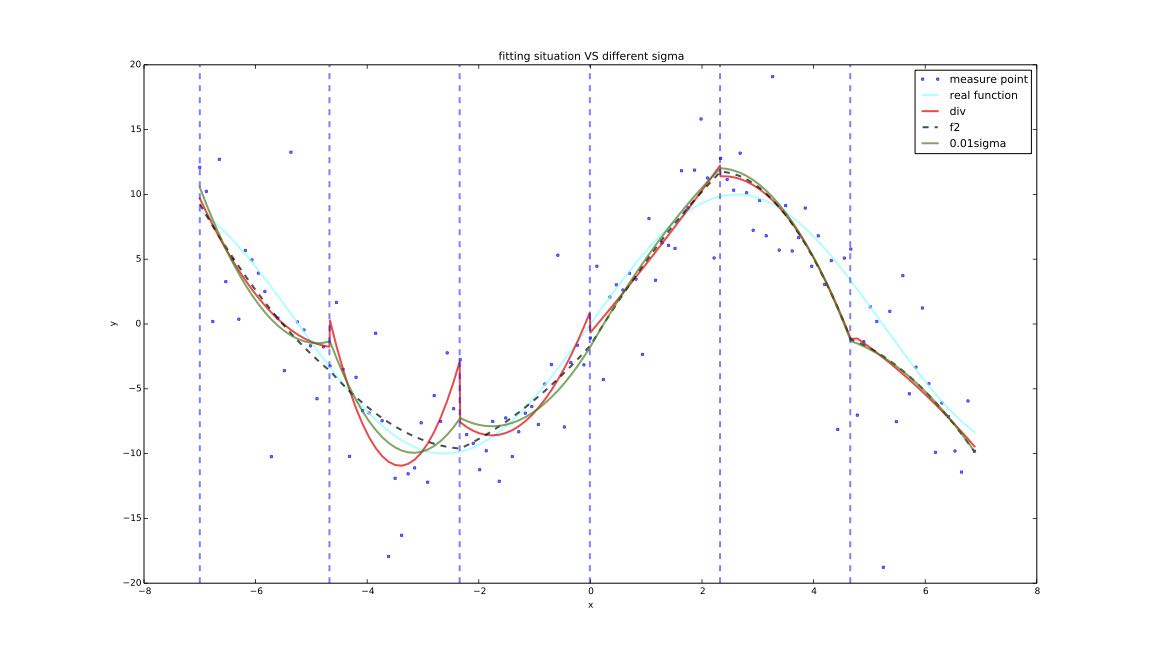
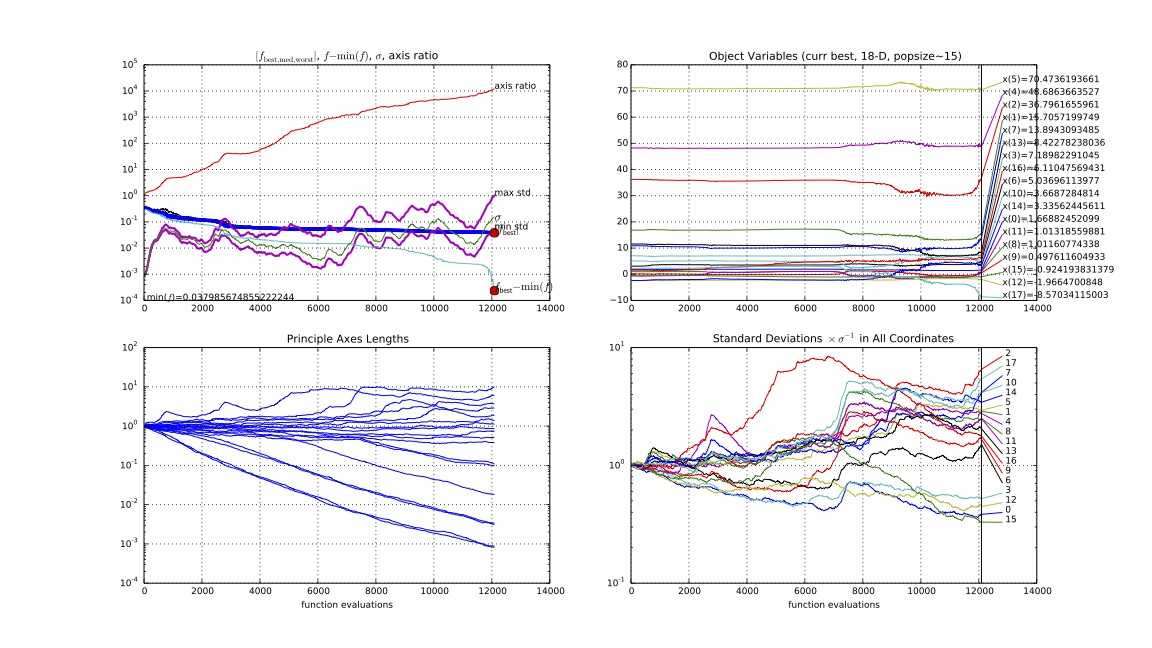
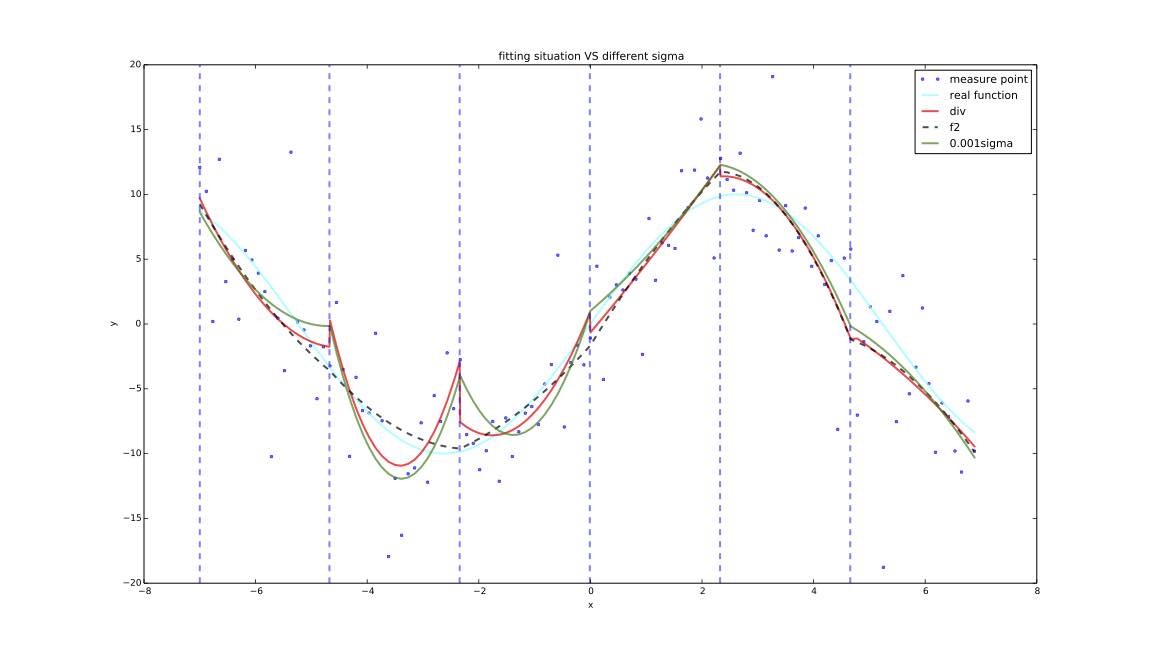
$\sigma=0.001$，迭代次数为806
$$拟合情况接近div，但代价较小$$
$\sigma=0.0001$，迭代次数为207 $$拟合情况接近div，但代价很小 $$

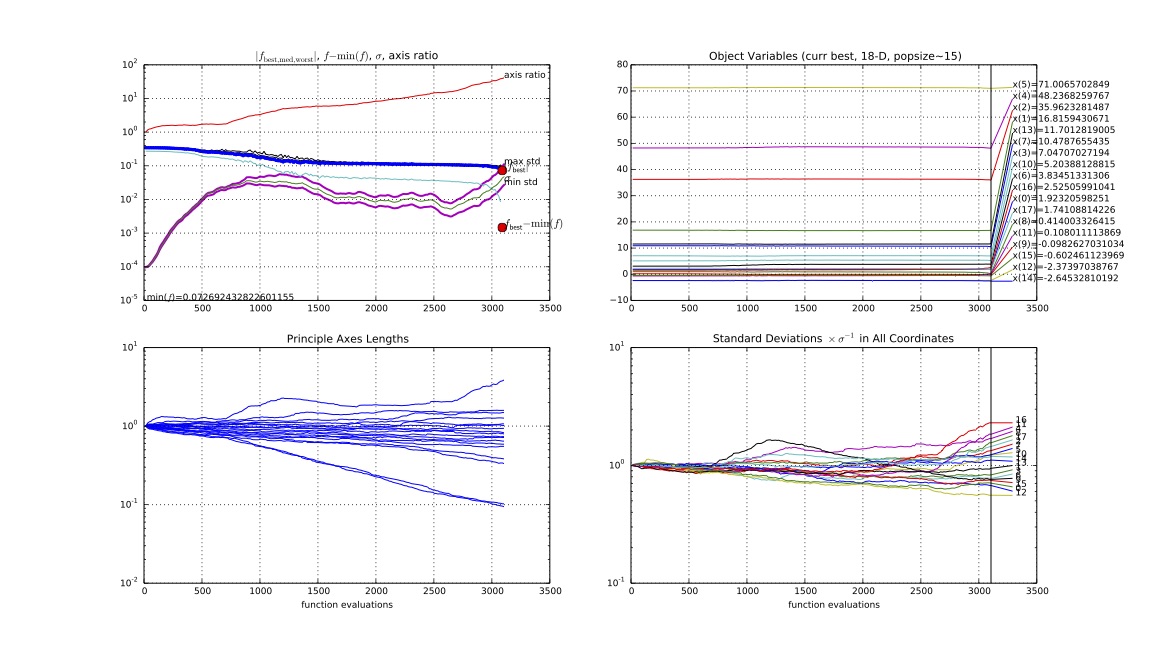
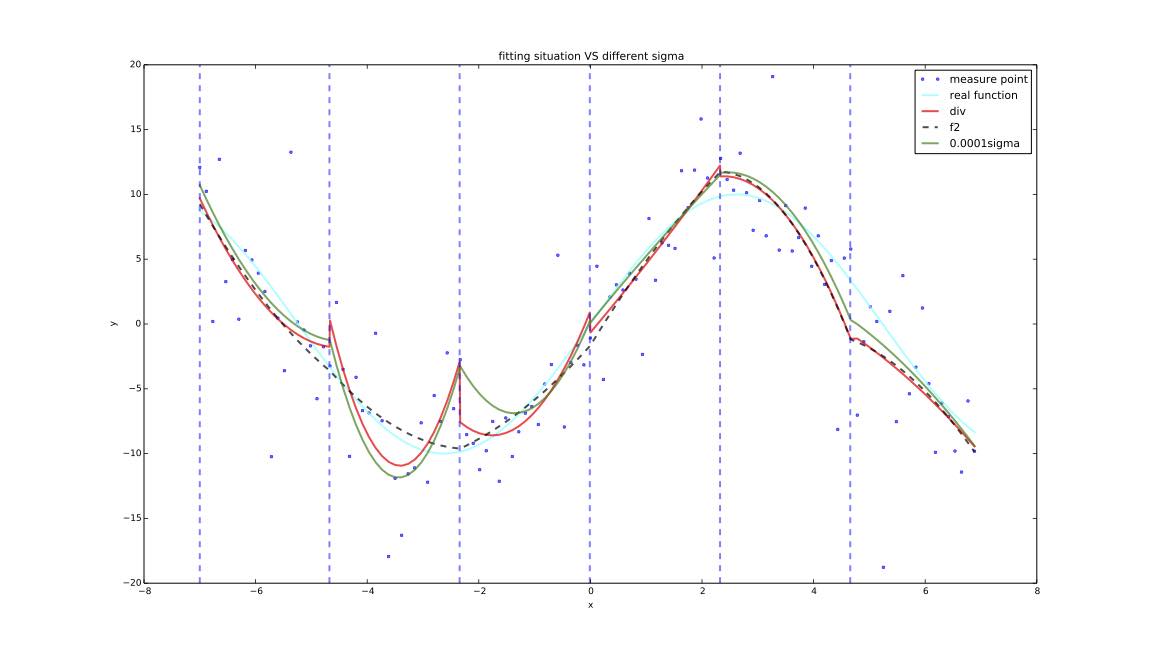
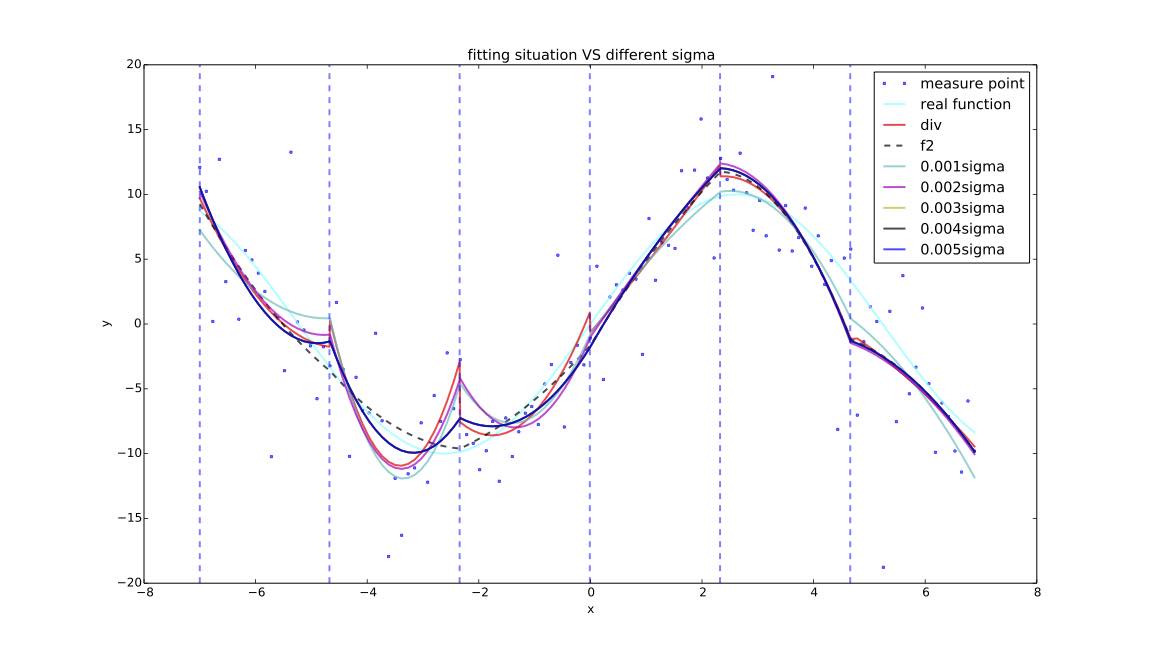
综上，集中$\sigma$=[0.001,0.002,0.003,0.004,0.005],迭代次数如下：

$\sigma$	iteration countiter
0.001	697
0.002	1056
0.003	2501
0.004	2323
0.005	2220